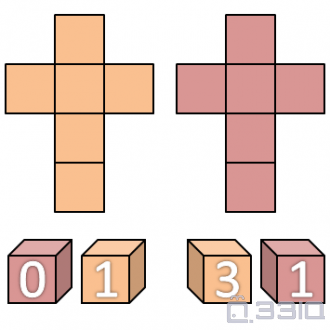
距離上次仙蹤招收弟子已經過去三個月了,雲夢仙蹤正在舉辦一年一度的外門大比。其中戊成功築基,榮獲冠軍,而乙和庚身為上品靈根,都突破到了練氣後期,而中品靈根的弟子還只是練氣中期,看來第二和第三就是乙和庚兩個人了。
庚的武技是概率神拳,攻擊時有30%概率觸發二次攻擊,並且擊中後有45%概率眩暈目標2回合。在對決時總是先手攻擊。
請問庚第一回合沒暈住乙的概率是多少?

經典的三門問題變版,非常容易做錯:
三扇門,兩扇裡面是空的,一扇裡面是車。
這次來了三個參與者甲、乙、丙,他們一人選擇了一扇門。這時候主持人打開了丙的門,告訴他,你的是空的,你走吧。然後問甲是否要換門,此時甲是否需要換門呢?

小周和小喬輪流拿圍棋棋子,總共361顆棋子。規定每次拿的下限是1顆棋子,上限是n顆棋子,(10≥n>1,n是正整數)誰拿到最後一枚棋子就算勝利。
起始n為4,為了增加難度,每人都有一次改變上限n的權利(可以不使用該權利),需在自己輪次時改變上限,然後自己取棋。先使用權利者必須要在拿走棋子總數量一半前使用,后使用權利者必須要在拿走棋子總數量2/3前使用。
假設小周和小喬足夠聰明,小喬選擇先手,最終結局是怎麼樣的?

俄羅斯有這樣一個數學故事:甲、乙兩人共養一群羊,過了一段時間后,他們決定去賣。決定這樣定價:每隻羊的售價就是羊的總只數。買完之後決定這樣分錢:甲先拿十元,乙再拿十元,如此輪流。最後甲拿過之後,剩餘不足10元,由乙拿去。請問當乙拿完最後的錢后,甲該給乙多少錢他們才能把這筆錢平均分?

有一種決鬥方式叫俄羅斯輪盤賭。用一把有6個彈槽的左輪手槍,在其中一個彈槽中放入一顆子彈,快速旋轉轉輪,再把它合上。參與決鬥的兩個人輪流對準自己的頭部開槍,三回合之內就會有一人死亡。雙方勝率都是50%,遊戲絕對公平。
那麼問題來了:在轉輪的連續3個彈槽中放入子彈,旋轉併合上。雙方都不知道子彈位置。假設你不想死(好像是廢話),你應該選擇先開槍還是后開槍呢?

在自由王國,有10名犯人被抓進監獄,現一共有紅,藍,黃色帽子若干被戴到犯人頭頂,每個犯人能看到其他人帽子的顏色,而不能看到自己的。規定監獄長隨機挑選犯人猜自己帽子的顏色,且只能說出一個顏色,說對的人可以釋放,說不對的繼續拘留。每個犯人可以聽到其他犯人說的顏色。犯人們可以在事前商量策略,假設每個人都可以為了更多人釋放執行策略,那麼最多可保證多少人釋放?

新一屆的總統選舉即將舉行,在20,000,000的投票者中只有1%的人支持現在的總統Sroan,所以他想用一種「民主」的方法來投票,他的提議如下:將所有的投票者分為n1個小組,每個小組中的人數都一樣,再將這些小組都分成n2個更小的子小組,這些小組中的人數也都一樣,再把他們在分成n3個更小的子子小組,以此類推。每一個(子)i小組按少數服從多數的原則選出第i-1級的代表,以此類推。Sroan能夠組織起這些小組並讓他的支持者分散在其中,使他最終獲勝嗎?