今天要上四堂课:数学、化学、语文、历史,已知:
1、第一堂课是语文或化学
2、第二堂课不是数学
3、第三堂课不是历史
4、化学是在第三或第四堂课
5、第四堂课是历史或化学
请问,四堂课的顺序到底是什么呢?

A 和 B 在赌场玩一个游戏,他们要协同作战与庄家对抗。游戏一轮一轮地进行,每一轮的规则都是一样的:首先 A 赌 0 和 1 当中的某个数字,然后 B 再赌 0 和 1 当中的某个数字,最后庄家给出 0 和 1 当中的某个数字;如果所有的三个数字都相同,则 A 和 B 获胜,否则庄家获胜。游戏前, A 和 B 可以商量一个对策,但游戏一旦开始,除了下赌注本身之外,两人不能再有其他任何形式的交流了。
容易看出,如果 A 和 B 都随机下注,他们只有 25% 的获胜概率。然而,如果两人事先约定,在每一轮中, B 总是跟着 A 下注, A 赌什么 B 就赌什么,那么他们获胜的概率就会提高到 50% 。但是,不管采用哪种方案,在最坏情况下,两人都有可能一次也不能获胜。
有意思的事情出现了。在游戏开始前两人商量策略的时候,两人突然意识到, B 有办法偷到庄家将会在游戏中使用的 01 序列。也就是说,游戏开始后,每一轮里庄家要出什么, B 都将会知道。但是,一旦 B 拿到了这个 01 序列, B 就不能和 A 交流了。在这样的条件下,两人能做得比刚才更好吗?能!比如说,两人可以保证在最坏情况下也有至少 50% 的获胜次数: B 可以在第 1, 3, 5, 7, … 轮游戏中赌下一轮庄家将会出的那个数(这相当于暗示了 A 下一轮赌什么),两人便能保证在第 2, 4, 6, 8, … 轮游戏中获胜了。
我们的问题是:假设游戏一共有 9 轮,设计一种策略使得 A 和 B 能够保证至少 6 次胜利。

在所有周长相等的长方形中,正方形拥有最大的面积;在所有周长相等的平面图形中,圆拥有最大的面积;在所有表面积相等的长方体中,正方体拥有最大的体积;在所有表面积相等的立体图形中,球拥有最大的体积。所有这类问题的答案都是越对称的图形越好吗? George Pólya 在 Mathematical Discovery 一书中的第 15 章里举了下面这个例子。
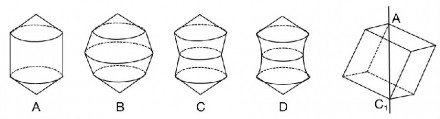
在给定圆周上选取四个点构成一个四边形,那么正方形的面积一定是最大的吗?答案是肯定的。只要有哪个点不在相邻两点之间的圆弧的中点处,我们都可以把它移动到这段圆弧的中点处,使得整个图形的面积变得更大。好了,我们现在的问题是,在球面上选取八个点构成一个顶点数为 8 的多面体,那么正方体一定是体积最大的吗?

假设你有 n 枚外观完全相同的硬币,它们的重量分别为 1g, 2g, 3g, …, ng 。有意思的是,这一次,你已经知道了各枚硬币的重量,而且你也已经把重量值标在了这些硬币上。但是,由于我不知道各枚硬币的重量,因此我希望你能向我证明,你所标的重量值是正确的(我知道这些硬币的重量是从 1 克到 n 克,我只是不知道哪个硬币对应哪个重量)。
你唯一能用的工具就是一架天平。每一次,你可以任意选择一枚或多枚硬币,放在天平的左侧,再从剩下的硬币中任意选择一枚或多枚硬币,放在天平的右侧(注意,你只能在天平上放硬币,不能放别的东西)。一个有意思的问题是,为了向我证明你所标的重量值都是对的,你最少需要使用多少次天平?

有位王子被巫婆下了咒,这个咒语使王子沉睡数千年,据说在远方的森林里有着红、橘、黄、绿、蓝、黑、白七个矮人,而他们的手上都有一颗苹果,但是请注意!美味苹果只有在说真话的诚实矮人的手上,说谎话的骗子矮人手上拿着的是毒苹果,如果想要唤醒王子,就只能给他吃美味苹果,请根据以下矮人说的每句话,判别谁手上拿着的是美味苹果?
红矮人:“黑矮人拿着的是美味苹果喔。”
橘矮人:“本大爷挖到了金块喔。”
黄矮人:“我和橘矮人是同一类的人。”
绿矮人:“山上的天气变化无常 昨天还下了大雨。”
蓝矮人:“我和白矮人不是同一类的人。”
黑矮人:“我和绿矮人可不是同一类的人。”
白矮人:“红矮人手上拿着的才是美味苹果。”
橘矮人:“美味苹果总共有三个。”