【数学寻宝迷踪2】暗藏玄机的数学题
神兽学校的这次数学期末考试,是由轻飘飘老师亲自出题的,非常简单。
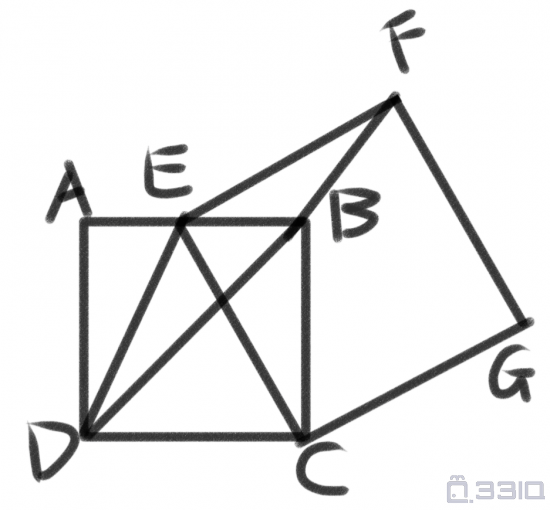
学霸暖宝宝做到了最后一道大题:如图,正方形ABCD的边AB的中点为E,连接CE。以CE为边,向右上方作正方形CEFG。连接DF。若AB=2,求三角形DEF的面积。
暖宝宝心里乐开了花,这次满分又稳拿了。
他略微想了一下便开始作答:
延长EB,过F作EB的延长线的垂线,交EB于H。
易证△CBE≌△EHF。
S△DEF=EB×F点与D点的高度差÷2=1×(FH+AD)÷2=1×(EB+AD)÷2=1.5。
那么他计算出的答案与正确答案相比如何?

在春运高峰时,某客运中心售票大厅站满等待买票的旅客,为保证售票大厅的旅客安全,大厅入口处旅客排队以相等速度进入大厅按次序等待买票,买好票的旅客及时离开大厅。按照这种安排,如果开10个售票窗口,5小时可使大厅内所有旅客买到票;如果开12个售票窗口,3小时可使大厅内所有旅客买到票,假设每个窗口售票速度相同。现在大厅入口处旅客速度增加到原速度的1.5倍,在2小时内使大厅中所有旅客买到票,按这样的安排至少应开售票窗口数为?

A、B、C、D、E、F六个人进行比赛,每次比赛为1对1,且每两个人只能比赛1次,每个人都进行了3场比赛。若获胜则积3分,平局积1分,失败积0分。比赛结束后,A积9分,B积2分,C积5分,F积7分。已知B和D之间、C和E之间、D和E之间没有比赛过。则D和E分别积几分?

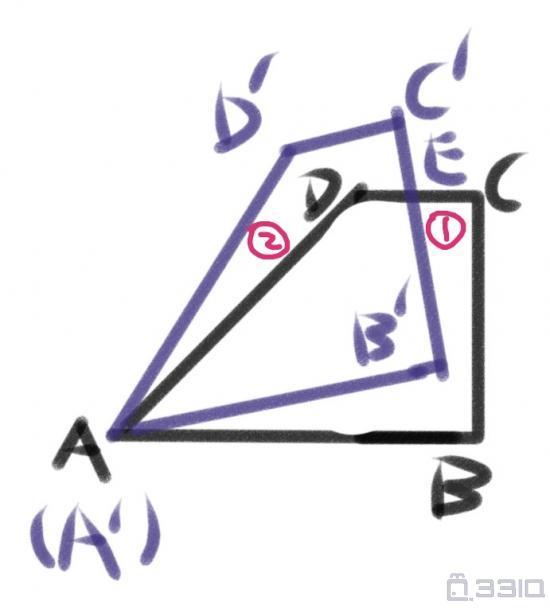
在△ABC与△A1B1C1中,已知AB<A1B1,BC<B1C1,CA<C1A1。
则下列五个结论中,正确结论的个数为?
①△ABC的边BC上高的长度一定小于△A1B1C1的边B1C1上高的长度。
②△ABC的边BC上的中线长度一定小于△A1B1C1的边B1C1上的中线长度。
③△ABC的面积一定小于△A1B1C1的面积。
④△ABC的外接圆半径一定小于△A1B1C1的外接圆半径。
⑤△ABC的内切圆半径一定小于△A1B1C1的内切圆半径。

在集合S上定义运算○,它满足以下两个条件:
(1)x○x=x,对一切x∈S都成立。
(2)(x○y)○z=(y○z)○x,对一切x,y,z∈S都成立。
问运算○是否满足结合律和交换律?
注:结合律指(x○y)○z=x○(y○z),交换律指x○y=y○x,对一切x,y,z∈S都成立。

四个连续正整数的积可以是完全平方数吗?可以是完全立方数吗?
注:完全平方数指的是某个整数的平方,如1,4,9,16,25,36,49...完全立方数指的是某个整数的三次方,如1,8,27...