【數學尋寶迷蹤2】暗藏玄機的數學題
神獸學校的這次數學期末考試,是由輕飄飄老師親自出題的,非常簡單。
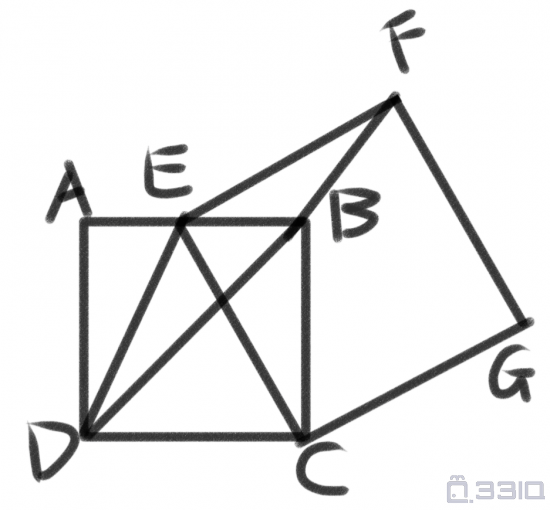
學霸暖寶寶做到了最後一道大題:如圖,正方形ABCD的邊AB的中點為E,連接CE。以CE為邊,向右上方作正方形CEFG。連接DF。若AB=2,求三角形DEF的面積。
暖寶寶心裡樂開了花,這次滿分又穩拿了。
他略微想了一下便開始作答:
延長EB,過F作EB的延長線的垂線,交EB於H。
易證△CBE≌△EHF。
S△DEF=EB×F點與D點的高度差÷2=1×(FH+AD)÷2=1×(EB+AD)÷2=1.5。
那麼他計算出的答案與正確答案相比如何?

在春運高峰時,某客運中心售票大廳站滿等待買票的旅客,為保證售票大廳的旅客安全,大廳入口處旅客排隊以相等速度進入大廳按次序等待買票,買好票的旅客及時離開大廳。按照這種安排,如果開10個售票窗口,5小時可使大廳內所有旅客買到票;如果開12個售票窗口,3小時可使大廳內所有旅客買到票,假設每個窗口售票速度相同。現在大廳入口處旅客速度增加到原速度的1.5倍,在2小時內使大廳中所有旅客買到票,按這樣的安排至少應開售票窗口數為?

A、B、C、D、E、F六個人進行比賽,每次比賽為1對1,且每兩個人只能比賽1次,每個人都進行了3場比賽。若獲勝則積3分,平局積1分,失敗積0分。比賽結束后,A積9分,B積2分,C積5分,F積7分。已知B和D之間、C和E之間、D和E之間沒有比賽過。則D和E分別積幾分?

在△ABC與△A1B1C1中,已知AB<A1B1,BC<B1C1,CA<C1A1。
則下列五個結論中,正確結論的個數為?
①△ABC的邊BC上高的長度一定小於△A1B1C1的邊B1C1上高的長度。
②△ABC的邊BC上的中線長度一定小於△A1B1C1的邊B1C1上的中線長度。
③△ABC的面積一定小於△A1B1C1的面積。
④△ABC的外接圓半徑一定小於△A1B1C1的外接圓半徑。
⑤△ABC的內切圓半徑一定小於△A1B1C1的內切圓半徑。

在集合S上定義運算○,它滿足以下兩個條件:
(1)x○x=x,對一切x∈S都成立。
(2)(x○y)○z=(y○z)○x,對一切x,y,z∈S都成立。
問運算○是否滿足結合律和交換律?
註:結合律指(x○y)○z=x○(y○z),交換律指x○y=y○x,對一切x,y,z∈S都成立。

四個連續正整數的積可以是完全平方數嗎?可以是完全立方數嗎?
註:完全平方數指的是某個整數的平方,如1,4,9,16,25,36,49...完全立方數指的是某個整數的三次方,如1,8,27...