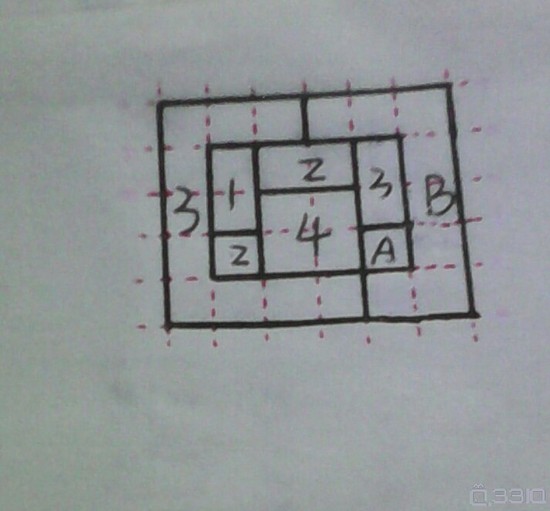
小世主有一块菜地(如图所示的五边形ABC'D'D,其中ABCD为正方形,A'BC'D'是由ABCD绕点B顺时针旋转30度得到的。连接C'C并延长交DD'于点E。)。已知区域C'D'E的面积比区域CED的面积大(2-√3)平方米。设图中阴影区域面积为S阴,正方形菜地的面积为S正。
小世主一共有辣椒、玉米、茄子、黄瓜和芹菜这五种蔬菜,为了合理利用这块菜地,他想出三种方案:
方案一:若2S阴>S正,则只在阴影区域种植两种蔬菜-玉米和辣椒;若2S阴≤S正,则不能在阴影区域种植辣椒和茄子。
方案二:若S阴/2<S正-3,则不能在阴影区域种植茄子和黄瓜;若S阴/2≥S正-3,则必须在空白区域种植玉米和芹菜。
方案三:若S阴<1.7平方米,则不能在空白区域种植芹菜。
在五种蔬菜都被种植的情况下,小世主选择在空白菜地种植( ).
(可能的参考值:√3≈1.7320508075689)

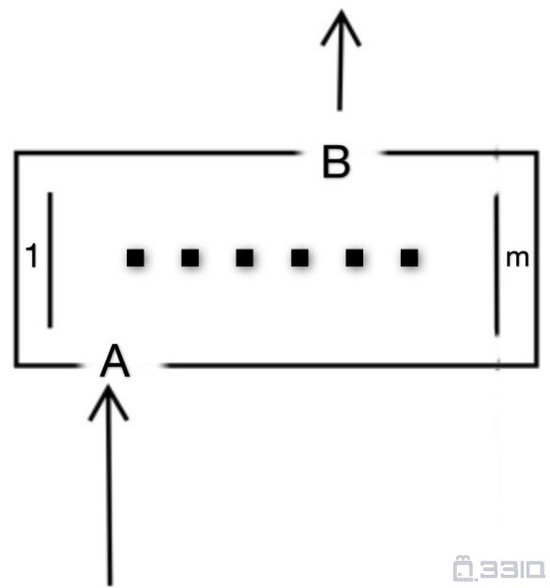
如图所示,有5个模拟人要依次通过一个区域,从A入B出。该区域包括m(m<20)个子通道,其中,有5个未知通道安装攻击系统,在毫无防备的情况下,模拟人是无法通过这5个通道。现给予2张库洛牌:梦(具有预知子通道是否安全的功能)和盾(抵抗所有的攻击和伤害),每张牌只能使用2次。在两张牌的次数全部用完的时候,5个人顺利通过该区域的概率P的最小值为63/275,则P的最大值为( ).
(注:①每一个人只能使用1张牌;②每一个所选的子通道不能有重复;③所谓的模拟人可以相互交流,预知到危险通道的前者必须将不能通过的子通道传送给后者,而通过子通道的模拟人是无法返回进行交流;④.不考虑预知到通过重复的通道;⑤.使用盾牌的2个模拟人先通过。)

某地有两种繁殖策略,支配者和分配者。支配者可为得到一个繁殖区域而战斗,如果他们获胜,将会培育出10个后代。另外一个选择是与其他人共享该区域,每人可以培育出5个后代。企图与支配者共享区域的分配者将会被强迫离开该区域,但他们仍然可以发现一个新的区域。假设分配者们在遇到支配者之后都非常谨慎,总是去周围寻找下次可以共享的区域,但是由于耽误了时间分配者只能制造出3个后代。支配者始终可以强迫分配者离开该区域,并培育出10个后代。支配者遇到支配者会有50%的机会取胜,如果失败,他们将不再繁殖。每个人都不能改变策略。
问题:如果支配者和分配者的总数为2000,那么应该有多少个支配者?