����Ϊ�۷������⣬��û���������ĿȨ�ޣ�ֻ����ЧOTF��Ա���ܲμ��۷�������
����n��n��3�����ε�ÿ������Ⱦ�Ϻ졢�̡�����ɫ֮һ��ʹ�����������������㲻ͬɫ����ÿ����ɫ�����ٳ���һ�Ρ�
�Ƿ������һЩ�Խ��߽���n���ηֳ�n−2�������Σ���ÿ�������ε������������ͬɫ��

��ͼ��ij������չ������36����������չ����ɣ�ÿ��������չ�ң�ָ�й����ߵ�С�����Σ���������ͨ����ij�ι��߲�Ը�����Ѳι۹���չ�ң�ͨ��ÿ����������һ�Σ�����ֻ�ܴӹ����߽�����һ�����䣬��ô�������ܲι۶��ټ�չ�ң�

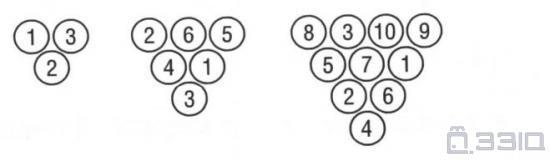

һ����ѧ����������ĺ����Ǻ����ļ�ֵ��������������˵��������λ���
����ѡ����һ�������Σ���ÿ���ߵij��ȶ���������
�㣬���װ��Ķ��Ӳ������Ҹ����������ε��ܳ������㣬���İ���Ů�����������Ҹ��������������
��Ȼ���Ƕ��������в��ܵ���ѧ�ң��Ҹҿ϶������ǿ���һ���ҳ������εĸ��߳�����
�����ǵĸ���������ÿ������Ӧ����Ϣ�����Ͱ��������������̸����
������ ������������֪���ܳ����Ҳ����ƶϳ����ߵij��ȡ���
�������� �� �Ҳ�֪���ܳ�����ֻ֪������Ҳ����ƶϳ����߳���Ҳ�����ǵĸ�������ȷ�ģ������վ�Ӧ�ú�������
������ ���ޣ�����Ҫ��������֪�����ߵij����ˡ���
�������� �� �ţ�������Ҳ֪���ˡ���
���������ε����߳���Ϊ���٣�







